The Point of Contention with Standard Cosmology

Not a week (or day) goes by without someone reporting the latest grand discovery supporting our standard model of cosmology, only to be supplanted the following week by an equally exciting and captivating observation claiming that our view of the origin and evolution of the Universe is clearly wrong. So which is it? Does the balance of evidence favor our current cosmological paradigm, or does it refute it, and what impact do new data have?

To understand what has brought us to this unsettled position, it can help to first describe as precisely as possible the specific reason for this disagreement. Though well-meaning, the many voices offering explanations to the public and the scientific community tend to focus on the symptoms (see e.g. refs. [1, 2, 3]), rather than addressing what is actually happening.

Today, cosmology is rich in data, a far cry from its genesis a century ago, when those daring to study this wild, unchartered frontier could only rely on speculation at best. It is fair to say, however, that after a century of work, certain tenets – if not outright facts – have ossified into an essential backbone for virtually all of cosmology. The vast majority of experts in this field consider this foundation to be unassailable. We all know how dangerous such a stance can be, since dogma has a habit of eventually failing, only to be replaced by new dogma. Yet the growing hubbub of disagreement being heard today does not impact these starting points for constructing a working model of the Universe, which are unquestionably accepted by nearly everyone working in this field.

The standard model's starting points

Among these tenets or facts, the most prominent examples include the following: (i) Einstein’s theory of general relativity is the correct description of gravity to use in building cosmic spacetime. There are some, of course, who believe that his field equations are incomplete, and an even (much) smaller minority of self-described, outright Einstein apostates. (ii) We have learned from Copernicus’s example that humanity does not occupy some privileged position (or epoch in time) in the cosmos, so the latter must be homogeneous and isotropic. These two simple symmetries are embodied in the universally accepted “cosmological principle.” (iii) Today, virtually all cosmology is thus based on one of the three most important and famous solutions to Einstein’s equations, known as the Friedmann-Lemaître-Robertson-Walker (FLRW) metric [Figure 1]. This metric, which yields the “interval” (ds) in terms of the time elapsed and distance between two points in spacetime, is the description of space and time consistent with both Einstein’s theory and the two basic symmetries.

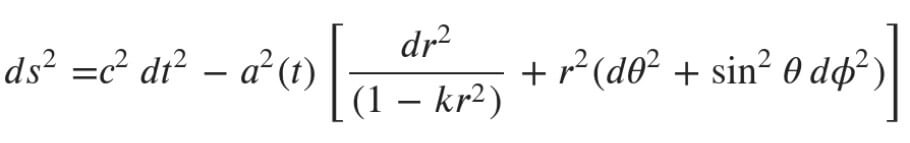
But this is the point at which the general consensus begins to unravel, and here is the specific reason for the growing tension and debate. Einstein’s field equations [Figure 2] account for the geometry of spacetime (on the left-hand side) in response to the energy and momentum of all components of the cosmos (on the right). Though not obvious, these equations are merely a four-dimensional version of the more familiar Poisson’s equation, which describes the gradient of a field (on the left) created by the source, such as the density of matter (on the right).

In March 1936, in the Journal of The Franklin Institute [4], Einstein himself described the left-hand side of his equations as “fine marble,” but the right side as only “low-grade wood,” meaning that the geometry was perfectly reliable, while the choice of energy-momentum tensor was somewhat arbitrary and often uncertain.

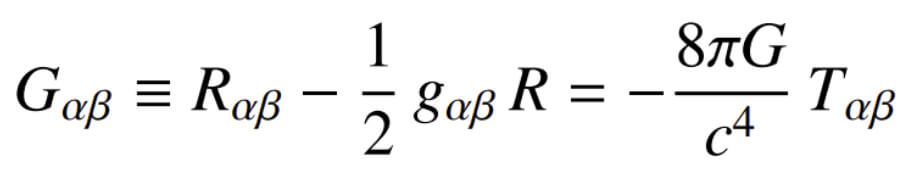
Unfortunately, this dichotomy translates directly into the FLRW metric universally used to describe cosmological phenomena. Its spacetime interval is written in terms of so-called comoving coordinates that never change. Actual, physical distances are obtained from them by multiplying comoving lengths by a universal expansion factor called a(t) [see Figure 1] (since the cosmological principle does not allow a(t) to vary in space; i.e., given that the Universe is presumably homogeneous, it can only be a function of time). Think of dots painted on an inflated balloon. Two such points separated by a constant fraction of the balloon’s circumference have fixed comoving coordinates (i.e., the fraction of a circumference), but their physical separation increases as the balloon expands.

Imprecise knowledge of the properties of the expansion factor a(t)

The poorly known form of the expansion factor a(t) is the culprit in this story – the reason why the abundance of data today is wreaking havoc with the standard model. Its unspecified dependence on time is Einstein’s “low-grade wood,” whose origin is directly traceable to the right-hand side of his field equations. Accordingly, the growing tension and uncertainty concerning our model of the Universe derive not from the presence of a(t), but from our imprecise knowledge of its value and evolutionary profile.

Not unreasonably, the standard model is completely based on the FLRW metric. Hardly anyone would take issue with this. The problem, though, is that general relativity offers very little guidance on what a(t) should be. The standard model filled this vacuum of knowledge empirically, patching together an assortment of early – and highly imprecise – observations to construct a “reasonable” right-hand side of the field equations, by deducing all of the possible constituents in the cosmic fluid that could contribute to the energy and momentum sourcing the spacetime geometry [5]. These include baryonic matter (which we see in galaxies and inside our bodies), non-baryonic matter (inferred from gravitational lensing and the dynamics of stars within galaxies), radiation and an unknown “dark” energy that seemingly prevents the Universe from succumbing to a decelerated expansion. The latter is crudely put in by hand as a “cosmological constant” of unknown origin. In other words, the right side of the equation is “low-grade” because it is probably simplistic, possibly naive, and certainly unmotivated by any fundamental theory.

But a(t) is so pivotal to virtually every measurement in this field that any error in its form creates enormous disparities between the standard model’s predictions and our ever-improving observations. One can easily see its impact on the expansion rate (i.e., the Hubble constant), the luminosity distance (e.g. to Type Ia supernovae), the angular-diameter distance (to clusters and other large-scale structures), the redshift (e.g. to the last scattering surface where the cosmic microwave background was produced), and the age versus redshift relationship, which is now doing the most serious damage to the standard model following the JWST space telescope’s discovery of galaxies far too close to the big bang [6, 7, 8, 9].

The need to re-appraise the energy-momentum tensor giving rise to a(t)

Given this provenance, why should it then surprise anyone that the enormous body of high-precision measurements we have today is starting to reveal significant flaws in the poorly motivated assumptions made for the right-hand side of Einstein’s equations in the early, primitive days of standard cosmology? And yet, a sizable fraction of the scientific community – arguably still a majority – are clinging desperately to the status quo established over 30 years ago, as if those early guesses were undeniably correct so that the data must be wrong, or must be fitted to the basic model with simple tweaks. One is reminded of the dogged support for the Ptolemaic system on the part of ancient astronomers, who persisted in adding epicycle upon epicycle in order to explain the absurd behavior of planets in an Earth-centered model of the solar system.

No doubt, one dominant factor contributing to this reluctance to entertain an evolution in cosmology is the general confusion – or simply unawareness in many cases – regarding the distinction between the “fine marble” and “low-grade wood” underlying the standard model. To be clear, very few scholars, if any, are calling for a re-evaluation of FLRW. In reality, there is no serious alternative right now (and perhaps there never will be). When the standard model is criticized for failing to explain the data, the critics’ focus should be recognized as the need to re-appraise the energy-momentum tensor giving rise to a(t). By no means is it sacrosanct; it was cobbled together before anyone even knew how massively unrealistic its predictions would prove to be.

Overwhelming flaws of the standard model, exposed by more recent data

And the flaws exposed by more recent data are overwhelming, not merely cosmetic. In my recent review [10], I highlighted eight distinct areas where the discordance between the standard model’s predictions and the cosmological measurements is most pronounced. And as serious as these problems are, they are merely a subset of all the issues revealed by the recent data. A more extensive compilation, though already dated just a few years after its publication, may be found in Table 2 of ref. [11].

This list is incomplete because, as noted earlier, new discoveries are now being made at a remarkable pace. A sample of three papers published in just the past few months is sufficient to illustrate this point:

• After many years, the extended Baryonic Oscillation Spectroscopic Survey released its final, complete analysis of the sonic horizon measured in the Lyman-α forest and background quasars at an average redshift of z=2.334, corresponding to a time when the Universe was only about one-third of its current age [12]. The standard model’s predicted expansion rate and angular-diameter distance at this redshift differ so substantially from those measured by this survey [13] that the probability of this discordance being merely due to some stochastic variation is less than 3% [14]. This was a major international collaboration that continued for several years, compiling a catalog comprising hundreds of thousands of distinct sources. It would be unrealistic to claim that the data were somehow wrong. The problem lies with the expansion factor a(t) in the standard model, because both the problematic Hubble rate and the angular-diameter distance depend directly upon it – and nothing else.
• In the course of thirty years of checking and rechecking, simulations of the formation of large-scale structures in the Universe based on the standard model have shown that no features larger than about 200 to 300 megaparsecs should exist anywhere in the cosmos. Yet many reports of structures 10 times this size have been published in recent years [15, 16, 17]. The expansion factor a(t) in the standard model thus fails to explain how clusters of galaxies formed – not by percentage points, but by more than an order of magnitude [18].
• The expansion factor a(t) in the standard model predicts a period of significant deceleration in the early Universe, giving rise to numerous inconsistencies highlighted by the so-called “horizon problem,” among others. The data indicate that the microwave background temperature is identical in all directions, yet the standard model could not have allowed opposite sides of the Universe to have been in contact to facilitate such an equilibration. To patch things up (adding another epicycle on top of older epicycles), inflation was invented about 40 years ago, basically to ensure that the a(t) in the early Universe included a brief period of exponentiated expansion to explain what we see today. But when we consider what it would take for inflation to work in this way, we see that it clearly violates the energy conditions under general relativity [19], and therefore cannot realistically be a viable solution to the horizon (and other early-Universe) problems.

The sooner we acknowledge that the primitive energy-momentum tensor constructed in the standard model’s infancy is in serious conflict with the data, the sooner we can all get down to identifying the correct physics underlying the real expansion factor a(t).

This does not mean throwing away cosmology’s “fine marble.” The FLRW spacetime appears to be perfectly consistent with our most successful theory of gravity and the symmetries that make sense to the vast majority of cosmologists. It simply means that we need to find a better grade of wood to inform the temporal evolution of the expansion factor a(t) than what we’ve been struggling with for too many decades [20].